eTRCA

This script shows how to use eTRCA from PyntBCI for decoding c-VEP trials. The eTRCA method uses a template matching classifier where templates are estimated using averaging and task-related component analysis (TRCA).

The data used in this script come from Thielen et al. (2021), see references [1] and [2].

References

[1]

Thielen et al. (2021) From full calibration to zero training for a code-modulated visual evoked potentials brain computer interface. DOI: https://doi.org/10.34973/9txv-z787

[2]

Thielen, J., Marsman, P., Farquhar, J., & Desain, P. (2021). From full calibration to zero training for a code-modulated visual evoked potentials for brain–computer interface. Journal of Neural Engineering, 18(5), 056007. DOI: https://doi.org/10.1088/1741-2552/abecef

import os

import matplotlib.pyplot as plt
import numpy as np
import seaborn

import pyntbci

seaborn.set_context("paper", font_scale=1.5)

Set the data path

The cell below specifies where the dataset has been downloaded to. Please, make sure it is set correctly according to the specification of your device. If none of the folder structures in the dataset were changed, the cells below should work just as fine.

path = os.path.join(os.path.dirname(pyntbci.__file__))  # path to the dataset
subject = "sub-01"  # the subject to analyse

The data

The dataset consists of (1) the EEG data X that is a matrix of k trials, c channels, and m samples; (2) the labels y that is a vector of k trials; (3) the pseudo-random noise-codes V that is a matrix of n classes and m samples. Note, the codes are upsampled to match the EEG sampling frequency and contain only one code-cycle.

# Load data
fn = os.path.join(path, "data", f"thielen2021_{subject}.npz")
tmp = np.load(fn)
X = tmp["X"]
y = tmp["y"]
V = tmp["V"]
fs = int(tmp["fs"])
fr = 60
print("X", X.shape, "(trials x channels x samples)")  # EEG
print("y", y.shape, "(trials)")  # labels
print("V", V.shape, "(classes, samples)")  # codes
print("fs", fs, "Hz")  # sampling frequency
print("fr", fr, "Hz")  # presentation rate

# Extract data dimensions
n_trials, n_channels, n_samples = X.shape
n_classes = V.shape[0]

# Read cap file
capfile = os.path.join(path, "capfiles", "thielen8.loc")
with open(capfile, "r") as fid:
    channels = []
    for line in fid.readlines():
        channels.append(line.split("\t")[-1].strip())
print("Channels:", ", ".join(channels))

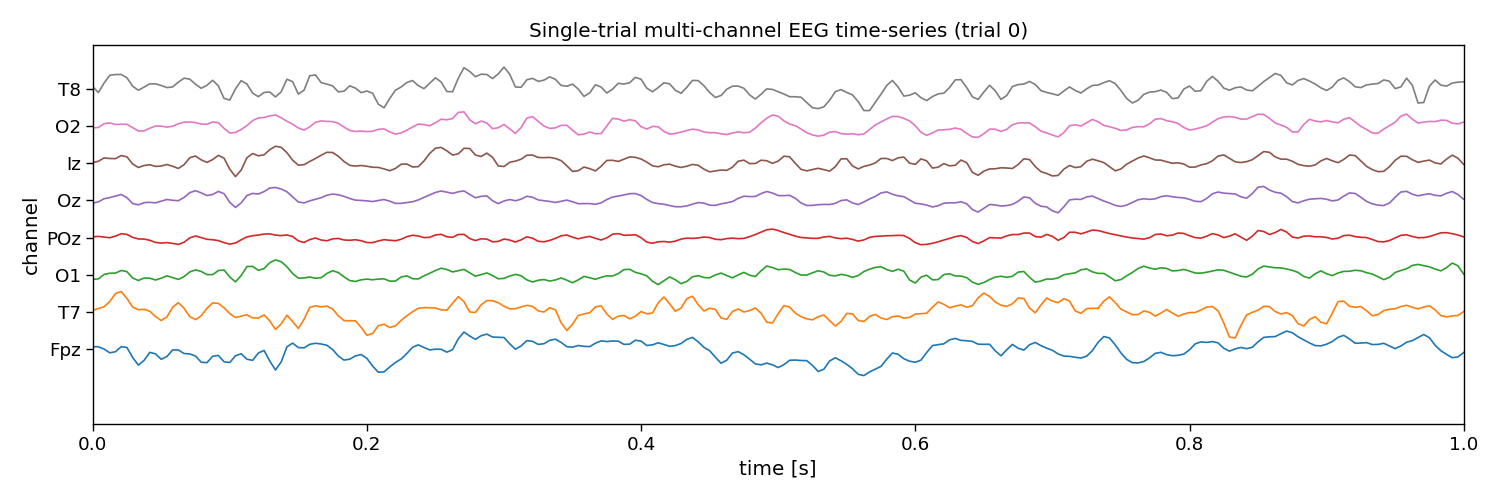
# Visualize EEG data
i_trial = 0  # the trial to visualize
plt.figure(figsize=(15, 5))
plt.plot(np.arange(0, n_samples) / fs, 25e-6 * np.arange(n_channels) + X[i_trial, :, :].T)
plt.xlim([0, 1])  # limit to 1 second EEG data
plt.yticks(25e-6 * np.arange(n_channels), channels)
plt.xlabel("time [s]")
plt.ylabel("channel")
plt.title(f"Single-trial multi-channel EEG time-series (trial {i_trial})")
plt.tight_layout()

# Visualize labels
plt.figure(figsize=(15, 3))
hist = np.histogram(y, bins=np.arange(n_classes + 1))[0]
plt.bar(np.arange(n_classes), hist)
plt.xticks(np.arange(n_classes))
plt.xlabel("label")
plt.ylabel("count")
plt.title("Single-trial labels")
plt.tight_layout()

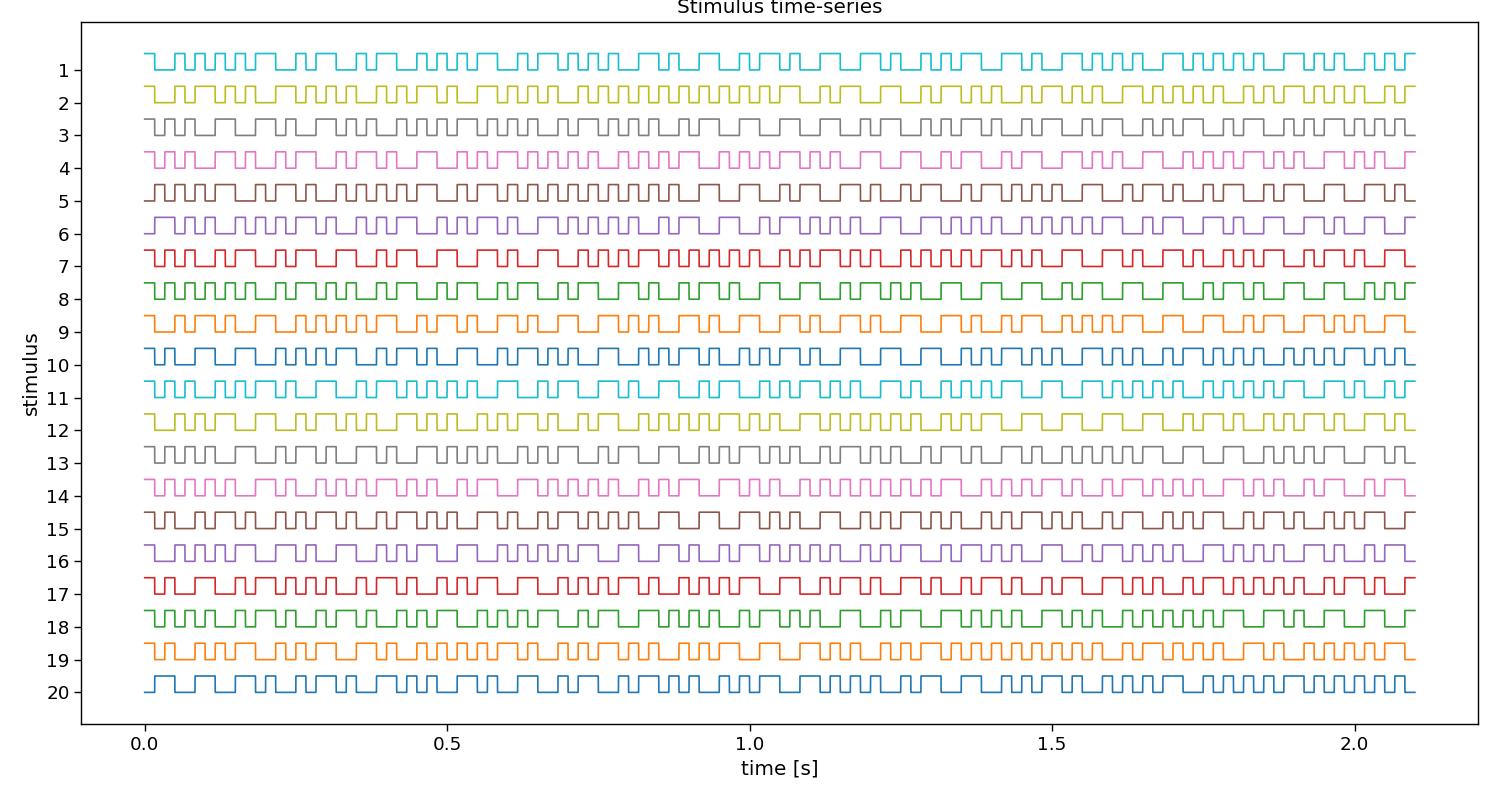
# Visualize stimuli
fig, ax = plt.subplots(1, 1, figsize=(15, 8))
pyntbci.plotting.stimplot(V, fs=fs, ax=ax, plotfs=False)
fig.tight_layout()
ax.set_title("Stimulus time-series")

• 
• 
• 

X (100, 8, 2520) (trials x channels x samples)
y (100,) (trials)
V (20, 504) (classes, samples)
fs 240 Hz
fr 60 Hz
Channels: Fpz, T7, O1, POz, Oz, Iz, O2, T8

Text(0.5, 1.0, 'Stimulus time-series')

ERP TRCA

The full ERP TRCA (eTRCA) pipeline is implemented as a scikit-learn compatible class in PyntBCI in pyntbci.classifiers.rCCA. All it needs are the lags if a circular shifted code is used (not used here) in lags, # the sampling frequency fs, and the duration of one period of a code as cycle_size. Additionally, eTRCA requires the argument ensemble to denote whether a separate spatial filter needs to be learned for each class.

When calling eTRCA.fit(X, y) with training data X and labels y, the template responses are learned as well as the spatial filters eTRCA.w_.

# Perform TRCA
cycle_size = 2.1  # 2.1 second code cycle length
etrca = pyntbci.classifiers.eTRCA(lags=None, fs=fs, cycle_size=cycle_size, ensemble=True)
etrca.fit(X, y)
print("w: shape:", etrca.w_.shape, ", type:", etrca.w_.dtype)

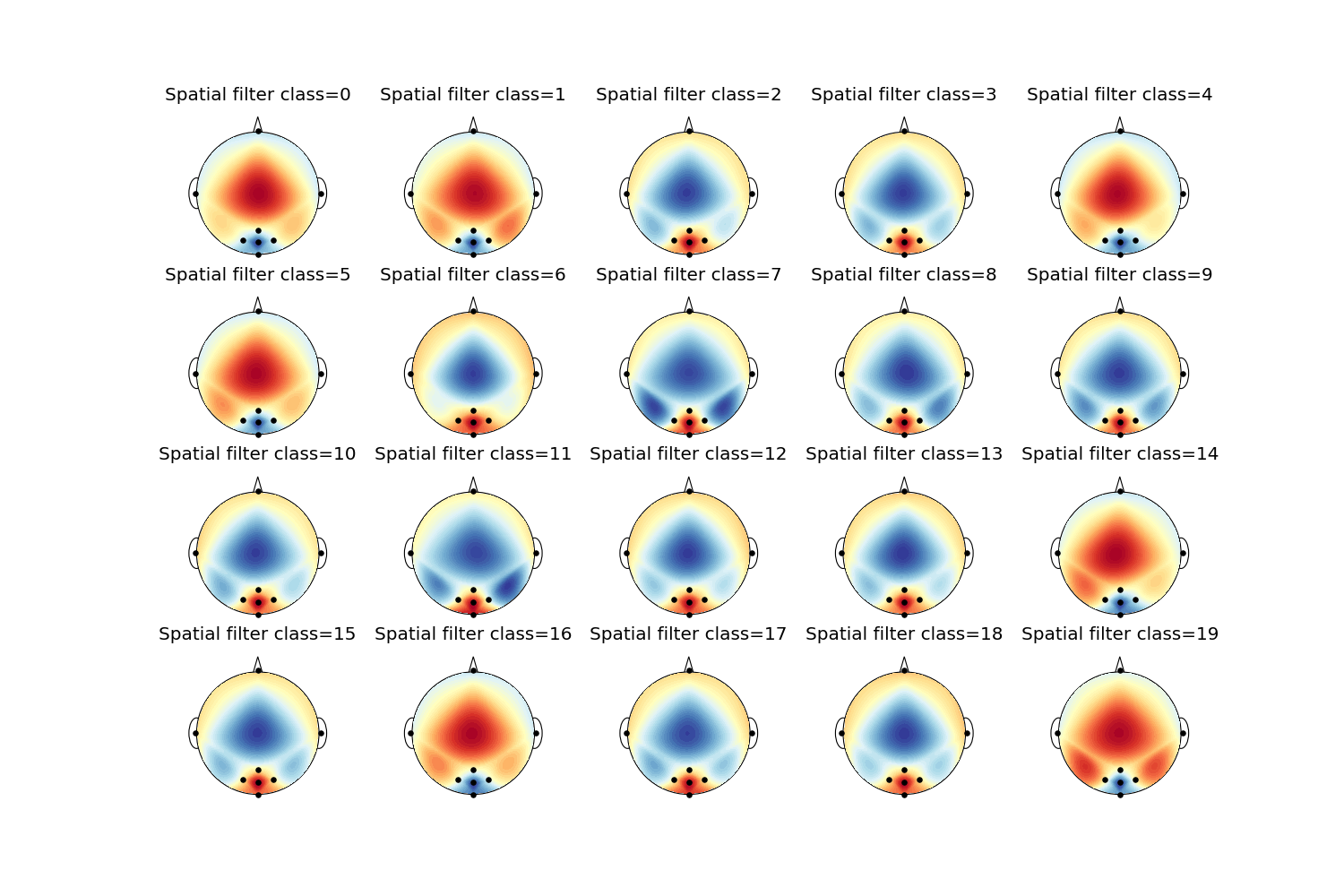
# Plot TRCA filters
if etrca.ensemble:
    nx = int(np.ceil(np.sqrt(n_classes)))
    ny = int(np.ceil(n_classes / nx))
    fig, ax = plt.subplots(ny, nx, figsize=(15, 10))
    ax = ax.flatten()
    for i_class in range(n_classes):
        pyntbci.plotting.topoplot(etrca.w_[:, 0, i_class], capfile, ax=ax[i_class])
        ax[i_class].set_title(f"Spatial filter class={i_class}")
else:
    fig, ax = plt.subplots(figsize=(5, 3))
    pyntbci.plotting.topoplot(etrca.w_, capfile, ax=ax)
    ax.set_title("Spatial filter")

w: shape: (8, 1, 20) , type: float64

Cross-validation

To perform decoding, one can call eTRCA.fit(X_trn, y_trn) on training data X_trn and labels y_trn and eTRCA.predict(X_tst) on testing data X_tst. In this section, a chronological cross-validation is set up to evaluate the performance of eTRCA.

trialtime = 4.2  # limit trials to a certain duration in seconds
intertrialtime = 1.0  # ITI in seconds for computing ITR
n_samples = int(trialtime * fs)

# Chronological cross-validation
n_folds = 5
folds = np.repeat(np.arange(n_folds), int(n_trials / n_folds))

# Loop folds
accuracy = np.zeros(n_folds)
for i_fold in range(n_folds):
    # Split data to train and valid set
    X_trn, y_trn = X[folds != i_fold, :, :n_samples], y[folds != i_fold]
    X_tst, y_tst = X[folds == i_fold, :, :n_samples], y[folds == i_fold]

    # Train template-matching classifier
    etrca = pyntbci.classifiers.eTRCA(lags=None, fs=fs, cycle_size=2.1, ensemble=True)
    etrca.fit(X_trn, y_trn)

    # Apply template-matching classifier
    yh_tst = etrca.predict(X_tst)

    # Compute accuracy
    accuracy[i_fold] = np.mean(yh_tst == y_tst)

# Compute ITR
itr = pyntbci.utilities.itr(n_classes, accuracy, trialtime + intertrialtime)

# Plot accuracy (over folds)
plt.figure(figsize=(15, 3))
plt.bar(np.arange(n_folds), accuracy)
plt.axhline(accuracy.mean(), linestyle='--', alpha=0.5, label="average")
plt.axhline(1 / n_classes, color="k", linestyle="--", alpha=0.5, label="chance")
plt.xlabel("(test) fold")
plt.ylabel("accuracy")
plt.legend()
plt.title("Chronological cross-validation")
plt.tight_layout()

# Print accuracy (average and standard deviation over folds)
print(f"Accuracy: avg={accuracy.mean():.2f} with std={accuracy.std():.2f}")
print(f"ITR: avg={itr.mean():.1f} with std={itr.std():.2f}")

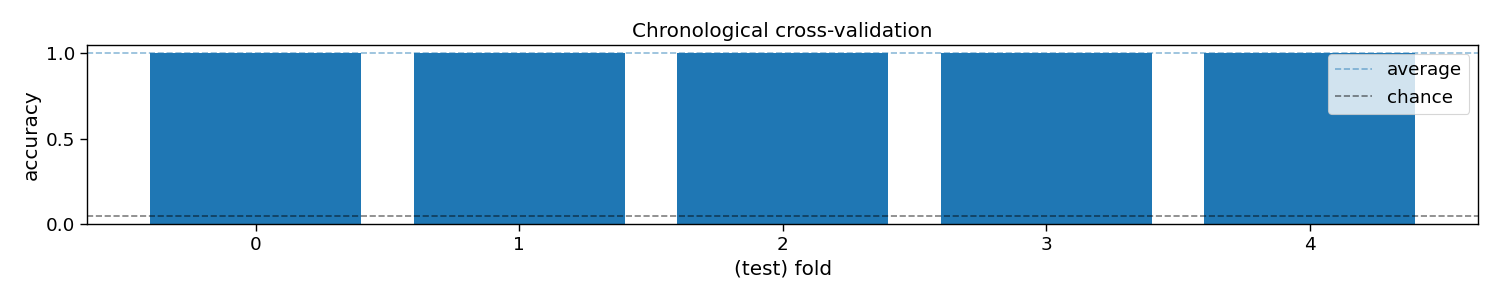
Accuracy: avg=1.00 with std=0.00
ITR: avg=49.9 with std=0.00

Learning curve

In this section, we will apply the decoder to varying number of training trials, to estimate a so-called learning curve. With this information, one could decide how much training data is required, or compare algorithms on how much training data they require to estimate their parameters.

trialtime = 4.2  # limit trials to a certain duration in seconds
n_samples = int(trialtime * fs)

# Chronological cross-validation
n_folds = 5
folds = np.repeat(np.arange(n_folds), int(n_trials / n_folds))

# Set learning curve axis
# Note, eTRCA needs at least 1 trial per class if lags=None
train_trials = np.arange(n_classes, 1 + np.sum(folds != 0))
n_train_trials = train_trials.size

# Loop folds
accuracy = np.zeros((n_folds, n_train_trials))
for i_fold in range(n_folds):

    # Split data to train and test set
    X_trn, y_trn = X[folds != i_fold, :, :n_samples], y[folds != i_fold]
    X_tst, y_tst = X[folds == i_fold, :, :n_samples], y[folds == i_fold]

    # Loop train trials
    for i_trial in range(n_train_trials):
        # Train classifier
        etrca = pyntbci.classifiers.eTRCA(lags=None, fs=fs, cycle_size=2.1, ensemble=True)
        etrca.fit(X_trn[:train_trials[i_trial], :, :], y_trn[:train_trials[i_trial]])

        # Apply classifier
        yh_tst = etrca.predict(X_tst)

        # Compute accuracy
        accuracy[i_fold, i_trial] = np.mean(yh_tst == y_tst)

# Plot results
plt.figure(figsize=(15, 3))
avg = accuracy.mean(axis=0)
std = accuracy.std(axis=0)
plt.plot(train_trials * trialtime, avg, linestyle='-', marker='o', label="eTRCA")
plt.fill_between(train_trials * trialtime, avg + std, avg - std, alpha=0.2, label="_eTRCA")
plt.axhline(1 / n_classes, color="k", linestyle="--", alpha=0.5, label="chance")
plt.xlabel("learning time [s]")
plt.ylabel("accuracy")
plt.legend()
plt.title("Learning curve")
plt.tight_layout()

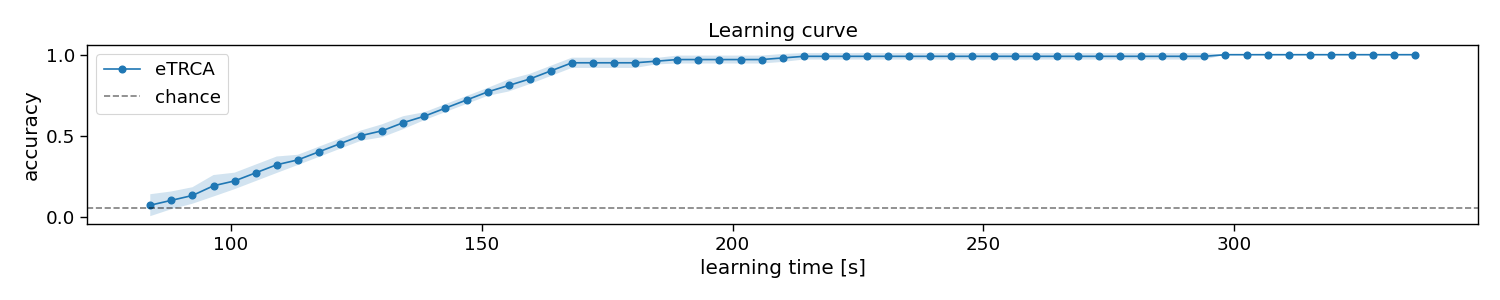
Decoding curve

In this section, we will apply the decoder to varying testing trial lengths, to estimate a so-called decoding curve. With this information, one could decide how much testing data is required, or compare algorithms on how much data they need during testing to classify single-trials.

trialtime = 4.2  # limit trials to a certain duration in seconds
intertrialtime = 1.0  # ITI in seconds for computing ITR
n_samples = int(trialtime * fs)

# Chronological cross-validation
n_folds = 5
folds = np.repeat(np.arange(n_folds), int(n_trials / n_folds))

# Set decoding curve axis
segmenttime = 0.1  # step size of the decoding curve in seconds
segments = np.arange(segmenttime, trialtime, segmenttime)
n_segments = segments.size

# Loop folds
accuracy = np.zeros((n_folds, n_segments))
for i_fold in range(n_folds):

    # Split data to train and test set
    X_trn, y_trn = X[folds != i_fold, :, :n_samples], y[folds != i_fold]
    X_tst, y_tst = X[folds == i_fold, :, :n_samples], y[folds == i_fold]

    # Setup classifier
    etrca = pyntbci.classifiers.eTRCA(lags=None, fs=fs, cycle_size=2.1, ensemble=True)

    # Train classifier
    etrca.fit(X_trn, y_trn)

    # Loop segments
    for i_segment in range(n_segments):
        # Apply classifier
        yh_tst = etrca.predict(X_tst[:, :, :int(fs * segments[i_segment])])

        # Compute accuracy
        accuracy[i_fold, i_segment] = np.mean(yh_tst == y_tst)

# Compute ITR
time = np.tile(segments[np.newaxis, :], (n_folds, 1))
itr = pyntbci.utilities.itr(n_classes, accuracy, time + intertrialtime)

# Plot results
fig, ax = plt.subplots(2, 1, figsize=(15, 5), sharex=True)
avg = accuracy.mean(axis=0)
std = accuracy.std(axis=0)
ax[0].plot(segments, avg, linestyle='-', marker='o', label="eTRCA")
ax[0].fill_between(segments, avg + std, avg - std, alpha=0.2, label="_eTRCA")
ax[0].axhline(1 / n_classes, color="k", linestyle="--", alpha=0.5, label="chance")
avg = itr.mean(axis=0)
std = itr.std(axis=0)
ax[1].plot(segments, avg, linestyle='-', marker='o', label="eTRCA")
ax[1].fill_between(segments, avg + std, avg - std, alpha=0.2, label="_eTRCA")
ax[1].set_xlabel("decoding time [s]")
ax[0].set_ylabel("accuracy")
ax[1].set_ylabel("ITR [bits/min]")
ax[0].legend()
ax[0].set_title("Decoding curve")
fig.tight_layout()

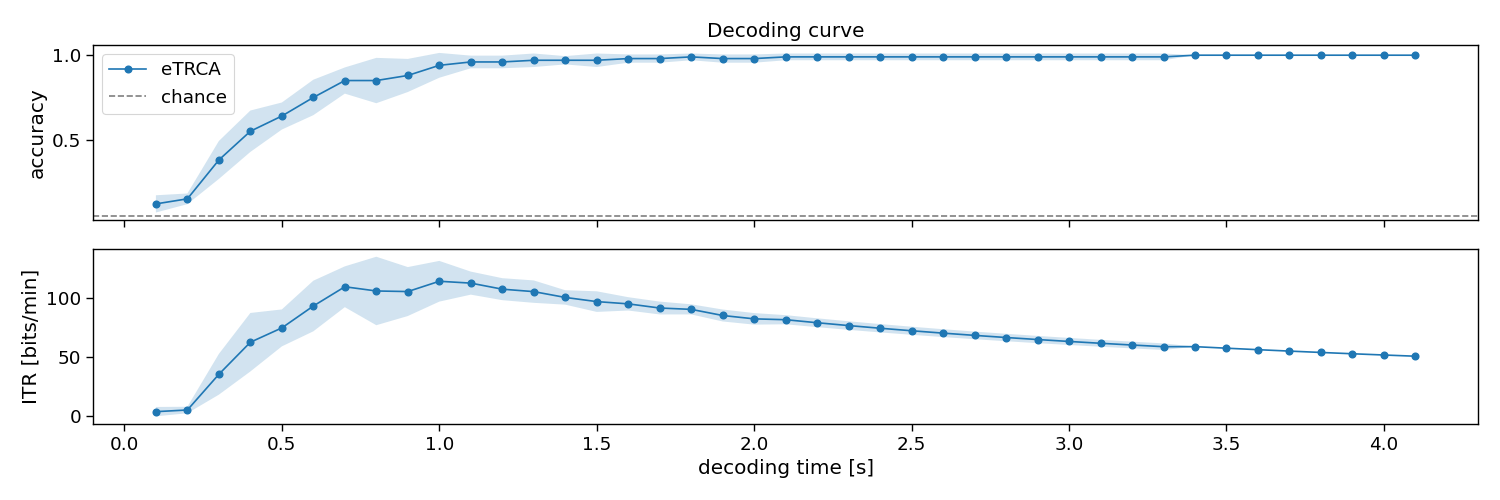
Analyse multiple participants

# Set paths
path = os.path.join(os.path.dirname(pyntbci.__file__))
n_subjects = 5
subjects = [f"sub-{1 + i:02d}" for i in range(n_subjects)]

# Set trial duration
trialtime = 4.2  # limit trials to a certain duration in seconds
n_trials = 100  # limit the number of trials in the dataset

# Chronological cross-validation
n_folds = 5
folds = np.repeat(np.arange(n_folds), int(n_trials / n_folds))

# Loop participants
accuracy = np.zeros((n_subjects, n_folds))
for i_subject in range(n_subjects):
    subject = subjects[i_subject]

    # Load data
    fn = os.path.join(path, "data", f"thielen2021_{subject}.npz")
    tmp = np.load(fn)
    fs = tmp["fs"]
    X = tmp["X"][:n_trials, :, :int(trialtime * fs)]
    y = tmp["y"][:n_trials]
    V = tmp["V"]

    # Cross-validation
    for i_fold in range(n_folds):
        # Split data to train and test set
        X_trn, y_trn = X[folds != i_fold, :, :], y[folds != i_fold]
        X_tst, y_tst = X[folds == i_fold, :, :], y[folds == i_fold]

        # Train classifier
        etrca = pyntbci.classifiers.eTRCA(lags=None, fs=fs, cycle_size=2.1, ensemble=True)
        etrca.fit(X_trn, y_trn)

        # Apply classifier
        yh_tst = etrca.predict(X_tst)

        # Compute accuracy
        accuracy[i_subject, i_fold] = np.mean(yh_tst == y_tst)

# Add average to accuracies
subjects += ["avg"]
avg = np.mean(accuracy, axis=0, keepdims=True)
accuracy = np.concatenate((accuracy, avg), axis=0)

# Plot accuracy
plt.figure(figsize=(15, 5))
avg = accuracy.mean(axis=1)
std = accuracy.std(axis=1)
plt.bar(np.arange(1 + n_subjects) + 0.3, avg, 0.5, yerr=std, label="eTRCA")
plt.axhline(accuracy.mean(), linestyle="--", alpha=0.5, label="average")
plt.axhline(1 / n_classes, linestyle="--", color="k", alpha=0.5, label="chance")
plt.table(cellText=[np.round(avg, 2), np.round(std, 2)], loc='bottom', rowLabels=["avg", "std"], colLabels=subjects,
          cellLoc="center")
plt.subplots_adjust(left=0.2, bottom=0.2)
plt.xticks([])
plt.ylabel("accuracy")
plt.xlim([-0.25, n_subjects + 0.75])
plt.legend()
plt.title("Decoding performance full dataset")
plt.tight_layout()

# Print accuracy
print(f"Average accuracy: {avg.mean():.2f}")

# plt.show()

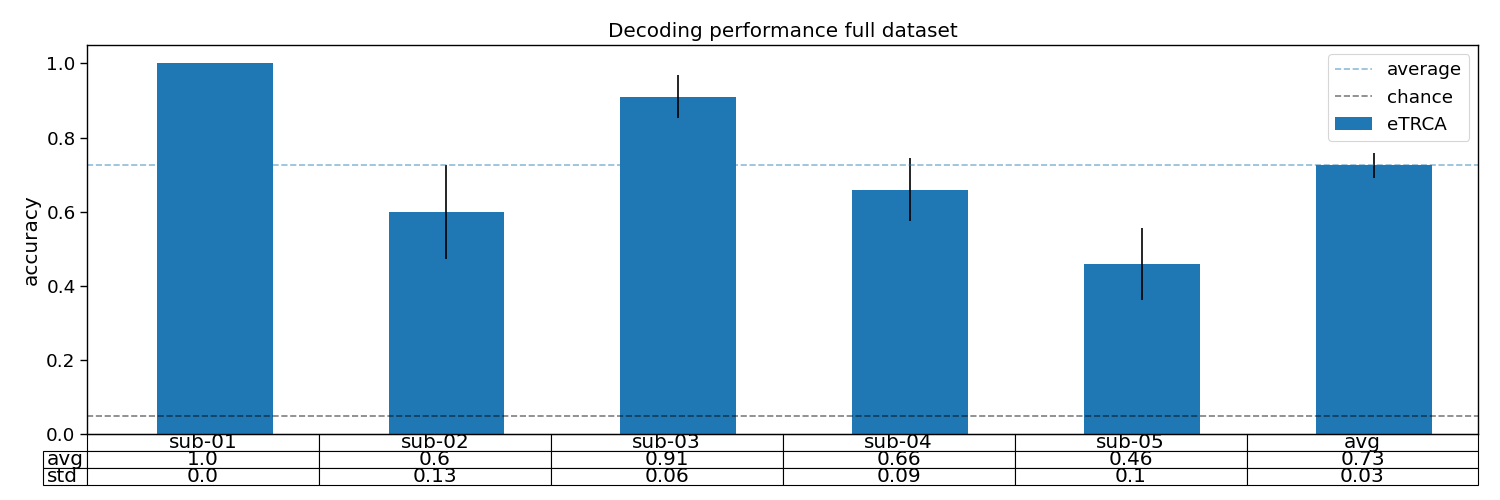
Average accuracy: 0.73