Stimulus optimization

This script shows how to optimize the stimulus presentation by means of selecting the optimal subset of stimuli from a set of candidate stimuli and how to select an optimal layout to allocate them to a stimulus grid. The methods to optimize such subset and layout were developed and evaluated in [1].

The data used in this script are simulated.

References

[1]

Thielen, J., Van Den Broek, P., Farquhar, J., & Desain, P. (2015). Broad-Band visually evoked potentials: re(con)volution in brain-computer interfacing. PloS one, 10(7), e0133797. DOI: https://doi.org/10.1371/journal.pone.0133797

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

import pyntbci

sns.set_context("paper", font_scale=1.5)

Simulated data

The cell below generated synthetic data. Specifically, we will generate a set of modulated Gold codes and use a convolution with a synthetic flash-VEP to generate simulated EEG template responses.

fs = 120  # Hertz
pr = 60  # Hertz
amplitude = 1.0  # microvolts
width = 0.020  # seconds
latency = 0.100  # seconds
encoding_length = 0.3  # seconds
n_channels = 1
snr = 0.5

# Generate codes
V = pyntbci.stimulus.make_gold_codes()
V = pyntbci.stimulus.modulate(V)
V = V.repeat(int(fs / pr), axis=1)
n_codes, n_samples = V.shape

# Generate structure matrices
M = pyntbci.utilities.encoding_matrix(V[:, np.newaxis, :], int(encoding_length * fs))

# Generate flash-VEP
time = np.arange(0, encoding_length, 1/fs)
r = amplitude * (1 - ((time - latency) / width)**2) * np.exp(-0.5 * ((time - latency) / width)**2)

# Generate template responses
T = r.dot(M.transpose((1, 0, 2)).reshape((-1, n_codes * n_samples))).reshape(n_codes, n_samples)
T /= np.std(T, axis=1, keepdims=True)  # normalize amplitudes

Optimize stimulus subset

The cell above generated 63 different codes and for each an expected template EEG response. In the following we assume we have a 4 x 8 matrix speller setup, for a total of 32 classes. Thus, we can select an optimal subset of 32 codes from the 63 available codes. This we will do by minimizing the maximum pair-wise correlation between templates within the subset.

n_random = 100000  # number of random "optimizations"

# Assumed speller matrix
matrix = np.arange(32).reshape(4, 8)
n_classes = matrix.size

# Compute correlation matrix
rho = pyntbci.utilities.correlation(T, T)
rho[np.eye(rho.shape[0]) == 1] = np.nan

# Optimize subset
optimized_subset = pyntbci.stimulus.optimize_subset_clustering(T, n_classes)
optimized = np.nanmax(rho[optimized_subset, :][:, optimized_subset])
optimized_vals = rho[optimized_subset, :][:, optimized_subset].flatten()
optimized_vals = optimized_vals[~np.isnan(optimized_vals)]

# Random subset
random_subset = []
value = 1  # maximum correlation
random = np.zeros(n_random)
for i in range(n_random):
    subset_ = np.random.permutation(T.shape[0])[:n_classes]
    random[i] = np.nanmax(rho[subset_, :][:, subset_])
    if random[i] < value:
        random_subset = subset_
        value = random[i]
random_vals = rho[random_subset, :][:, random_subset].flatten()
random_vals = random_vals[~np.isnan(random_vals)]

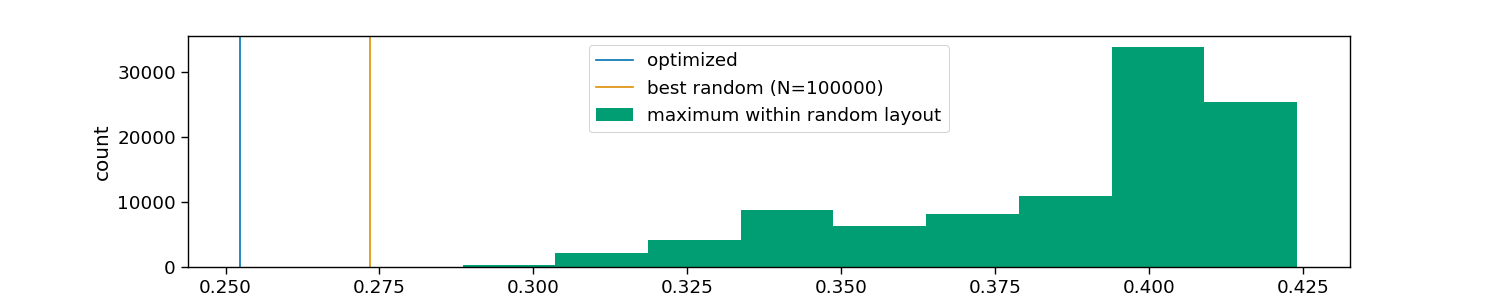
# Visualize tested and optimized layouts
colors = sns.color_palette("colorblind")
plt.figure(figsize=(15, 3))
plt.axvline(optimized, color=colors[0], label="optimized")
plt.axvline(random.min(), color=colors[1], label=f"best random (N={n_random})")
plt.hist(random, color=colors[2], label="maximum within random layout")
plt.legend()
plt.xlabel("maximum correlation across layouts")
plt.ylabel("count")

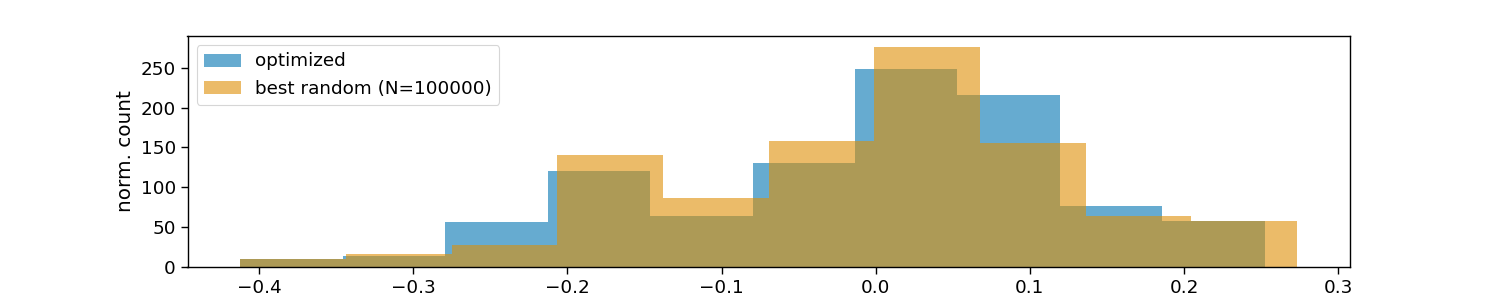
# Visualize optimized layouts
colors = sns.color_palette("colorblind")
plt.figure(figsize=(15, 3))
plt.hist(optimized_vals, 10, alpha=0.6, color=colors[0], label="optimized")
plt.hist(random_vals, 10, alpha=0.6, color=colors[1], label=f"best random (N={n_random})")
plt.legend()
plt.xlabel("maximum correlation within layouts")
plt.ylabel("norm. count")

• 
• 

Text(135.16666666666669, 0.5, 'norm. count')

Optimize stimulus layout

Now we have the optimal subset of 32 codes. Still, we could optimize how these are allocated to the 4 x 8 speller grid, such that codes that still correlate much are not placed at neighbouring cells in the grid.

# Select optimize subset
T = T[optimized_subset, :]

# Compute correlation matrix
rho = pyntbci.utilities.correlation(T, T)
rho[np.eye(rho.shape[0]) == 1] = np.nan

# Create neighbours matrix assuming 4 x 8 grid
neighbours = pyntbci.utilities.find_neighbours(matrix)

# Optimize layout
optimized_layout = pyntbci.stimulus.optimize_layout_incremental(T, neighbours, 50, 50)
optimized = np.nanmax(rho[optimized_layout[neighbours[:, 0]], optimized_layout[neighbours[:, 1]]])
optimized_vals = rho[optimized_layout[neighbours[:, 0]], optimized_layout[neighbours[:, 1]]].flatten()
optimized_vals = optimized_vals[~np.isnan(optimized_vals)]

# Random layout
random_layout = []
value = 1  # maximum correlation
random = np.zeros(n_random)
for i in range(n_random):
    layout_ = np.random.permutation(T.shape[0])
    random[i] = np.nanmax(rho[layout_[neighbours[:, 0]], layout_[neighbours[:, 1]]])
    if random[i] < value:
        random_layout = layout_
        value = random[i]
random_vals = rho[random_layout[neighbours[:, 0]], random_layout[neighbours[:, 1]]].flatten()
random_vals = random_vals[~np.isnan(random_vals)]

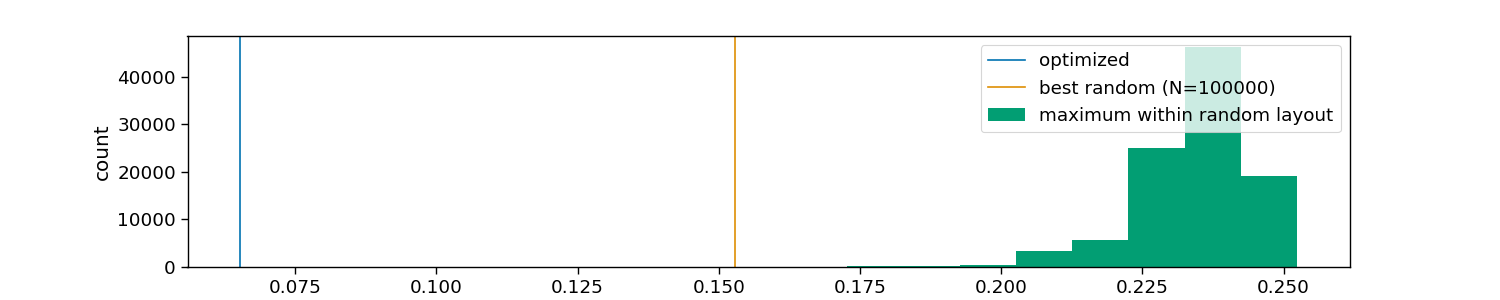
# Visualize tested and optimized layouts
colors = sns.color_palette("colorblind")
plt.figure(figsize=(15, 3))
plt.axvline(optimized, color=colors[0], label="optimized")
plt.axvline(random.min(), color=colors[1], label=f"best random (N={n_random})")
plt.hist(random, color=colors[2], label="maximum within random layout")
plt.legend()
plt.xlabel("maximum correlation across layouts")
plt.ylabel("count")

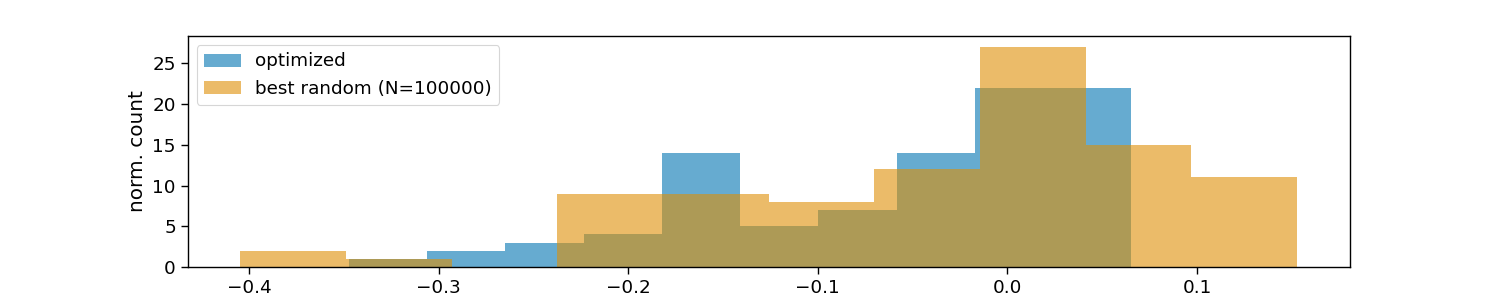
# Visualize optimized layouts
colors = sns.color_palette("colorblind")
plt.figure(figsize=(15, 3))
plt.hist(optimized_vals, 10, alpha=0.6, color=colors[0], label="optimized")
plt.hist(random_vals, 10, alpha=0.6, color=colors[1], label=f"best random (N={n_random})")
plt.legend()
plt.xlabel("maximum correlation within layouts")
plt.ylabel("norm. count")

# plt.show()

• 
• 

Text(146.91666666666669, 0.5, 'norm. count')